Building a Binary TTL Menorah
The Festival of LEDs
We celebrate Hanukkah in my household, and being the geek that I am, I thought it would be fun to create a digital version of the menorah (or chanukkiyah), which is the candelabra that is lit on each night of Hanukkah.
Each night, a different number of lights are illuminated. I figured I could connect switches to digital inputs, and then use those to control the number of lights. To make it a little extra nerdy, I would use three switches to input a binary number representing which night it was.
At first, I thought of building it using a microcontroller and coding it to read digital input pins (from the physical switches), and then output signals to LEDs to light up. However, I realized that using an MCU was a bit of overkill for this, and it would be more fun (and even geekier!) to do everything using pure digital logic (no code). So, in the spirit of Nand to Tetris I set out to create a digital circuit that only used transistor-transistor logic to perform the digital decoding of the switches (I briefly considered diode logic but determined that the voltage drops likely wouldn’t work to drive the LEDs).
Digital Logic
I don’t have the space for a full lesson, but there are many resources available for learning about digital logic. In short, we can use a transistor as a fundamental building block for creating circuits that can produce specific outputs in response to specific inputs.
The simplest of these circuits are known as logic gates, and then allow the computation of basic Boolean functions such as AND, OR, and NOT. These simple gates can be combined (by connecting the outputs of some gates to the inputs of others) to create larger circuits that can produce more complex outputs that respond to specific inputs. This is how computers “compute”; networks of transistors are connected together that can perform tasks such as arithmetic and memory storage.
A Menorah Counter
In my case, I wanted to create a digital circuit that would count out the days of Hanukkah. There are various counter / decoder circuits out there, but I set out to create my own without using something off the shelf.
To start, we note that there are only 8 possible states for the menorah (one for each night of Hanukkah). Lucky for us, 8 is a power of 2, so that means all 8 states can be represented with only 3 input switches, because 2 to the 3rd power is 8 (given some number n of binary inputs, the number of possible states is 2 to the nth power).
With that information, we can devise a table mapping possible input states to output states. The three switches are labeled “SW1”, “SW2”, and “SW3”, and we assume they go from least significant (SW1) to most significant (SW3). The lights are numbered from 1 to 8, each corresponding to the night of Hanukkah. Each night a new light is lit in addition to all the lights that were lit on previous nights:
| Night | Counter | SW3 | SW2 | SW1 | L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1st | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2nd | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3rd | 2 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4th | 3 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 5th | 4 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 6th | 5 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 7th | 6 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 8th | 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
You’ll notice that the switches count in a standard binary pattern, going from 000 (zero) to 111 (seven); the “counter” value gives the decimal equivalent. We normally think of Hanukkah as having a “first” night (not a “zeroth”), but fortunately we just need to mentally add or subtract 1 to convert between the “night” and “counter” values.
The output is not a simple representation of the input. We want to sequentially light turn on outputs with each successive binary input. In this way, it’s kind of like a counter mixed with a demultiplexer(?).
My approach was to take each light independently and figure out which input(s) caused the light to be on. In this way, we can wire each light back to its inputs independently of the other lights. Remember that each light, once lit, stays on for all the subsequent inputs. Here are the logical rules that dictate when each light is on:
| Light | SW3 | SW2 | SW1 | Condition |
|---|---|---|---|---|
| L1 | 0 | 0 | 0 | Always on! |
| L2 | 0 | 0 | 1 | SW1 OR SW2 OR SW3 |
| L3 | 0 | 1 | 0 | SW2 OR SW3 |
| L4 | 0 | 1 | 1 | (SW1 AND SW2) OR SW3 |
| L5 | 1 | 0 | 0 | SW3 |
| L6 | 1 | 0 | 1 | SW3 AND (SW1 OR SW2) |
| L7 | 1 | 1 | 0 | SW3 AND SW2 |
| L8 | 1 | 1 | 1 | SW3 AND SW2 AND SW1 |
Some interesting things from that table:
-
Because there are no nights where all the lights are unlit, that means that the first light is always on (it’s lit on the first, and all subsequent nights). Thus, there is no “logic” here that depends on the inputs!
-
For the second light, it is lit on all but the first night. Thus, any switch being on means it should be on, since the only time it’s off is when all of the switches are off.
-
Conversely, look at lights 5 through 8. All of these require (at a minimum) that SW3 be on, since SW3 is needed for the binary representation of 4, 5, 6, and 7 (remember, we’re off by one when we convert from binary count to night of Hanukkah).
So each light/night becomes a little logical puzzle (I’m getting flashbacks to Rocky’s Boots from my childhood) that you need to figure out. You need to match the switch inputs for that night (and all subsequent nights), while being selective enough to not match any earlier.
Recalling that we can build transistor circuits that compute values like AND and OR, we can directly express the Boolean logic above in circuitry.
(Exercise for the reader: it is also possible to perform a “negative logic” version of the table above, where the inputs and outputs are inverted. This would have been helpful if we were using pure transistors to wire our circuit, as NAND, NOR, and NOT are easier gates to build; fewer transistors are needed. In the end, I decided to use pre-fabricated gate chips, so I decided to stick with positive logic that is easier to follow conceptually.)
A Logical Circuit
Now it’s time to design a circuit that can represent our logical tables above. A quick reminder of some optimizations we can perform:
-
The “shamash”, or “helper candle” is lit every night. Thus, it does not need to be controlled by the logic and can simply be wired to input power at all times. I haven’t included this in the tables above for this reason, but we do need to include it in our circuit planning.
-
The first night’s candle (L1) is lit every night, because it is lit the first night, and all candles are lit for every subsequent night once lit. Thus, we can simply wire the first light to input power as it is never turned off.
-
Whenever we have a Boolean operation that is used in multiple places, we can wire it once and use its output to feed multiple inputs. For example, L7 uses SW3 AND SW2, while L8 uses SW3 AND SW2 AND SW1. Thus, we can build a circuit that computes SW3 AND SW2, and wire it’s output to both L7 and to the input of an AND gate that has SW1 as its other input.
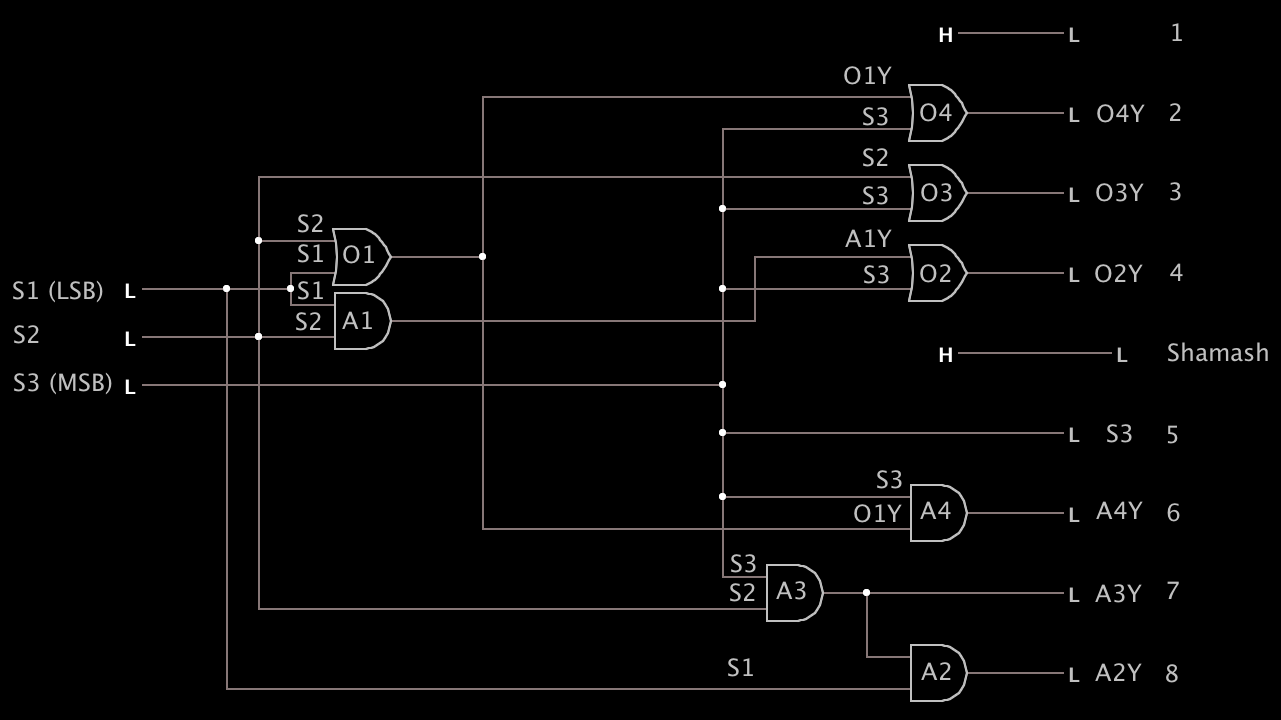
The diagram below shows a logical wiring diagram for the desired circuit. The switches are shown at left (SW1, SW2, and SW3), and the lights are shown at right (L1 through L8, plus the shamash).
The logic gates are numbered for uniqueness and prefixed with a letter (“A” for AND and “O” for OR). Following their data sheet conventions, the outputs are labeled with a “Y”.
To help make the diagram easier to follow, I labeled the “far end” of some wires so you can see where they come from without having to trace them all the way back to their source.
The “H” in the diagram just means logically “high” as in “power is on”. The first candle and shamash are wired directly to voltage.
Here is the logical diagram (click on it for a full-size image):
Designing the Circuit
As luck would have it, we only needed 4 AND gates and 4 OR gates for the complete design. This is great for us because you can buy packaged chips with multiple gates on them, and a common configuration is to have 4 gates on a chip. The AND gates are on the 7408 package (datasheet), and the OR gates are on the 7432 package (datasheet).
There are a few other real-world considerations that aren’t shown in the logical diagram. First, I added a fourth switch (SW4) that is only used for powering the entire system on and off. My battery pack had a switch on it, but just in case you used a power source that didn’t have its own switch, I figured this would be helpful.
Another is the use of a Darlington array in the circuit (part number ULN2803A, datasheet). The reasoning is that the logic that controls the circuit does not need a lot of current (we’re just switching binary values). But the end result is causing current to flow through the LEDs. The Darlington array allows us to cause a (relatively) high amount of current to flow while being controlled by a very small current (the output of the logic gates).
Finally, I put some small current-limiting resistors (150Ω) in line with each LED to ensure they stayed within range (datasheet says 30mA).
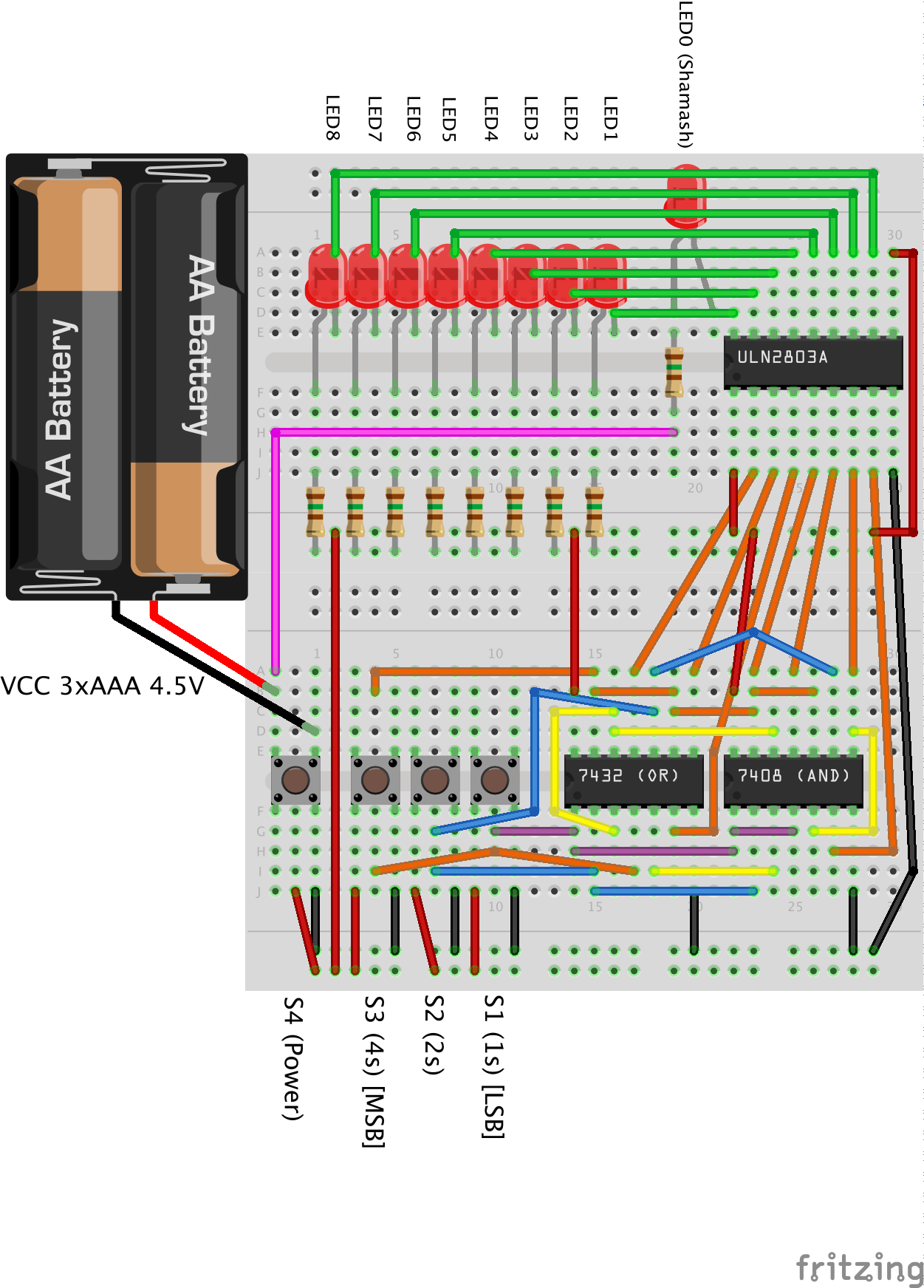
So, with all that said, here is a Fritzing diagram of a breadboard layout of the circuit. The layout takes 2 breadboards side-by-side to give me enough room for all of the DIP chips and still have a relatively compact arrangement:
Note that the switches shown there aren’t quite right; I’m using toggle switches that stay in position when pressed (and then reset when pressed a second time). The diagram shows momentary switches which aren’t useful for this as you don’t want to have to hold the buttons down to keep the lights lit. I just couldn’t find the right part in Fritzing.
Building the Circuit
With a plan in place, it was time to order some parts and build!
I found some frosted orange LEDs that looked like they would give off a nice glow (some LEDs are too directional). Of course, you can use any you happen to have lying around. I mixed in some red ones so there was some variety in the color.
Just about any 7400 logic should work; we’re not going for ultra-high speed or anything like that. The data sheets are linked above if you want to get the exact same one, but any compatible option should be fine.
I snapped two mini breadboards together and wired everything with jumpers. Here’s a picture of what it looks like (minus the power supply and power switch):
The layout isn’t a perfect match to the schematic, but the schematic was a good plan to follow, especially for the chip pinouts.
And here is a demo of the board in action. Note that I made this without a power switch (SW4) on the board, so it powers up as soon as the power supply is turned on.
Unfortunately, the light from the LEDs bleed into each other on the video, but in person it looks good! You can see me pressing the switches; most significant (SW3) is on the left, and least (SW1) is on the right. I count all the way up through the 8 possible binary states using the three switches.
And there you have it, a functioning binary menorah using only transistor logic!